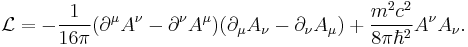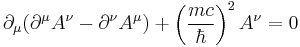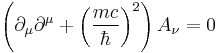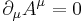Proca action

Quantum field theory
(Feynman diagram)
History of...
Background Gauge theory Field theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Crossing Charge conjugation Parity Time reversal
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin

In physics, in the area of field theory, the Proca action describes a massive spin-1 field of mass m in Minkowski spacetime. The field involved is a real vector field A. The Lagrangian density is given by:

$\mathcal{L}=-\frac{1}{16\pi}(\partial^\mu A^\nu-\partial^\nu A^\mu)(\partial_\mu A_\nu-\partial_\nu A_\mu)%2B\frac{m^2 c^2}{8\pi \hbar^2}A^\nu A_\nu.$

The above presumes the metric signature 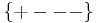$\lbrace%2B - - -\rbrace$ . Here, 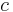$\! c$ is the speed of light and 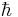$\hbar$ is the reduced Planck constant. In the dimensionless units commonly employed in theoretical physics, these may both be taken to be one.

The Euler-Lagrange equation of motion for this case, also called the Proca equation, is:

$\partial_\mu(\partial^\mu A^\nu - \partial^\nu A^\mu)%2B \left(\frac{mc}{\hbar}\right)^2 A^\nu=0$

which is equivalent to the conjunction of

$\left(\partial_\mu \partial^\mu%2B \left(\frac{mc}{\hbar}\right)^2\right)A_\nu=0$

with

$\partial_\mu A^\mu=0 \!$

which is the Lorenz gauge condition. The Proca equation is closely related to the Klein-Gordon equation.

The Proca action is the gauge-fixed version of the Stueckelberg action via the Higgs mechanism. Quantizing the Proca action requires the use of second class constraints.

The Proca action is named after Romanian physicist Alexandru Proca.